Overview
We demonstrate that challenging shortest path problems can be solved via direct spline regression from a neural network, trained in an unsupervised manner (i.e. without requiring ground truth optimal paths for training). To achieve this, we derive a geometry-dependent optimal cost function whose minima guarantees collision-free solutions. Our method beats state-of-the-art supervised learning baselines for shortest path planning, with a much more scalable training pipeline, and a significant speedup in inference time.
Method
Suppose that we wish to construct a loss function \(\mathcal{L}\) on a path parameterised by a set of parameters \(\theta\). A natural way to write this cost would be along the lines of $$ \mathcal{L}(\theta) = l(\theta) + \lambda * c(\theta) $$ where \(l\) is a length component, \(c\) is a collision component, and \(\lambda \in \mathbb{R}\) is a scaling hyperparameter.
We would like \(\mathcal{L}\) to have two properties. Firstly, \(\mathcal{L}\) should have minima in paths that are non-colliding and shortest possible. Secondly, \(\mathcal{L}\) should be differentiable, as we would like to train a neural network using SGD to solve shortest path problems. Let’s say we have a set of scenes over which we would like to optimize the parameters of our neural network. How shall we select \(\lambda\) such that the minima of \(\mathcal{L}\) are optimal? Turns out, this choice is not straightforward as \(\lambda\) depends on the scenes.
In our paper, we show that one can get rid of \(\lambda\) if \(c(\theta)\) is equal to the sum of the bounding sphere circumferences of all the objects \(\theta\) collides with. In our paper (Appendix A), we show that such cost yields paths that are shortest possible and non-colliding. Then, we also construct a differentiable version, which has minima in paths that are non-colliding and has bounded length offsets with respect to optimal paths in expectation.
Experiments
2D planning
In our first experiment, we compare our method with a naive cost formulation (i.e., with a fixed \(\lambda\)) on 150 random sphere & rectangle planning problems. Problems are generated such that a straight-line path is guaranteed to collide. We use bruthe-force optimisation to solve for optimal path paramteters \(\theta\) and in the process visualize the cost values at all possible \(\theta\) on a 2D plane. We use the single sphere planning problem in the image below (top-left) to tune \(\lambda\) for the naive cost.
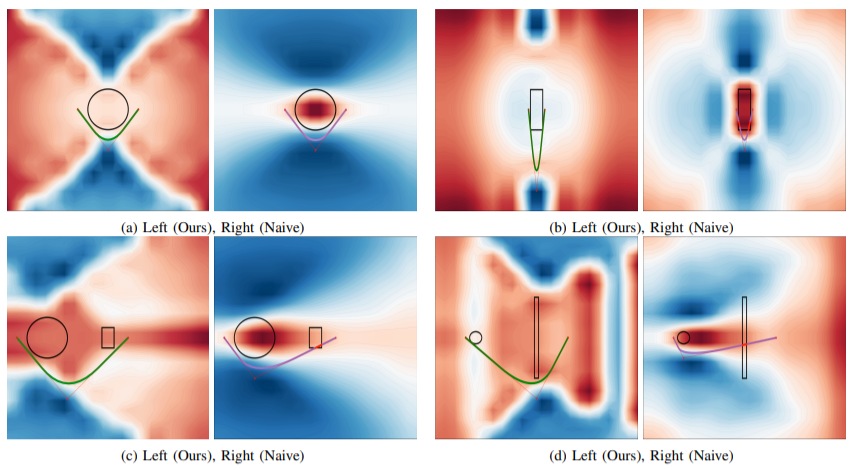
In the image above, our method successfully avoids the objects (left), while the naive cost, apart from the tuning problem, collides (right). Indeed, our method achieved a 100% success rate, while the naive cost performed around 79.33%.
Real-life demo
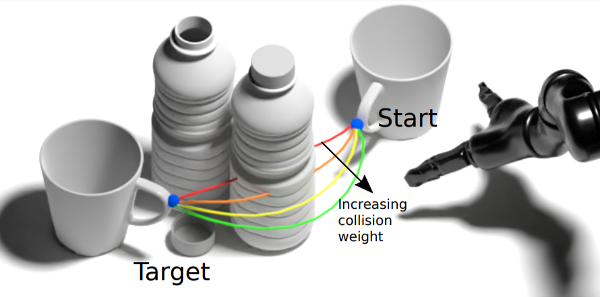
In this experiment, we demonstrate the usefulness of our cost for higher-dimensional planning problems using the CoppeliaSim simulator. For visualization purposes, instead of using a neural network to directly predict the pahts, we optimise our cost function with respect to the parameters of the cost per scene. This way, we can showcases how the path improves with each optimisation step.

In the first setup, we plan paths for a drone in a setting where the drone needs to finds its way around furniture. We observe that the resulting paths successfully avoid collisions.

In the next setup, we plan paths for a 6-DoF manipulator in presence of a cuboid obstacle. Again, we can see that the manipulator successfully plans around the obstacle.